Luyện tập Bài §3. Những hằng đẳng thức đáng nhớ, chương thơm I – Phxay nhân với phxay chia những đa thức, sách giáo khoa toán 8 tập một. Nội dung bài xích giải bài xích đôi mươi 21 22 23 24 25 trang 12 sgk toán 8 tập 1 bao hàm tổng vừa lòng cách làm, kim chỉ nan, phương pháp giải bài xích tập phần đại số bao gồm vào SGK toán để giúp đỡ các em học sinh học giỏi môn tân oán lớp 8.
Bạn đang xem: Bài 21 trang 12 sgk toán 8 tập 1
Lý thuyết
1. Bình phương thơm của một tổng
(left( A + B ight)^2 = A^2 + 2AB + B^2)
2. Bình phương thơm của một hiệu
(left( A – B ight)^2 = A^2 – 2AB + B^2)
3. Hiệu nhì bình phương
(A^2 – B^2 = left( A – B ight)left( A + B ight))
Dưới đó là Hướng dẫn giải bài xích trăng tròn 21 22 23 24 25 trang 12 sgk toán 8 tập 1. Các các bạn hãy tham khảo kỹ đầu bài bác trước khi giải nhé!
Luyện tập
pigeonholebooks.com reviews cùng với các bạn vừa đủ phương thức giải bài bác tập phần đại số 8 kèm bài bác giải chi tiết bài xích trăng tròn 21 22 23 24 25 trang 12 sgk tân oán 8 tập 1 của bài §3. Những hằng đẳng thức lưu niệm trong chương I – Phxay nhân với phnghiền phân chia các đa thức cho chúng ta tìm hiểu thêm. Nội dung chi tiết bài giải từng bài xích tập các bạn xem bên dưới đây:
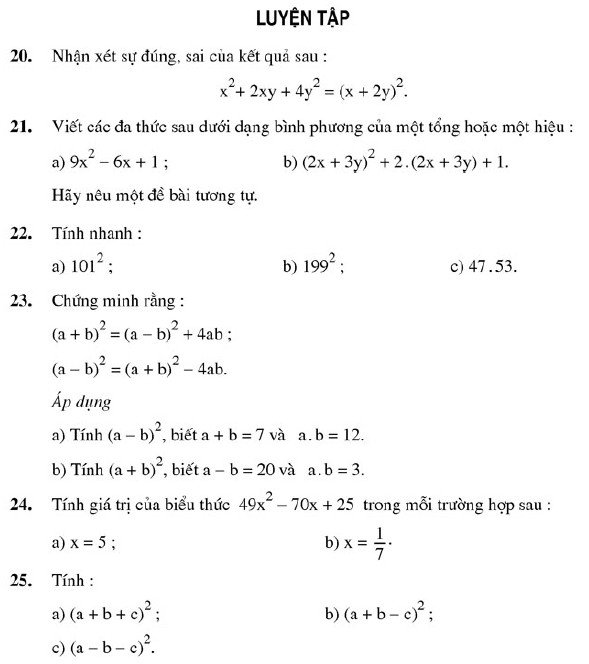
1. Giải bài bác 20 trang 12 sgk Toán thù 8 tập 1
Nhận xét sự đúng, sai của hiệu quả sau:
$x^2 + 2xy + 4y^2 = (x + 2y)^2$
Bài giải:
Ta có: $(x + 2y)^2$
$= x^2 + 2 . x . 2y + 4y^2$
$= x^2 + 4xy + 4y^2$
Nên tác dụng $x^2 + 2xy + 4y^2 = (x + 2y)^2$ là sai.
2. Giải bài bác 21 trang 12 sgk Tân oán 8 tập 1
Viết các nhiều thức sau bên dưới dạng bình pmùi hương của một tổng hoặc một hiệu:
a) $9x^2 – 6x + 1;$
b) $(2x + 3y)^2 + 2 . (2x + 3y) + 1.$
Hãy nêu một đề bài tựa như.
Xem thêm: Xem Phim Tiệm Bánh Hoàng Tử Bé, Phần 2 Tập 91 Vietsub + Thuyết Minh
Bài giải:
a) 9$x^2 – 6x + 1$
$= (3x)^2 – 2 . 3x . 1 + 1^2$
$= (3x – 1)^2$
Hoặc: $9x^2 – 6x + 1 = 1 – 6x + 9x^2 = (1 – 3x)^2$
b) $(2x + 3y)^2 + 2 . (2x + 3y) + 1$
$= (2x + 3y)^2 + 2 . (2x + 3y) . 1 + 1^2$
$= <(2x + 3y) + 1>^2$
$= (2x + 3y + 1)^2$
Đề bài xích tương tự: Viết các đa thức sau dưới dạng bình pmùi hương của một tổng hoặc một hiệu
$1 + 2(x + 2y) + (x + 2y)^2$
$4x^2 – 12x + 9$
3. Giải bài 22 trang 12 sgk Toán thù 8 tập 1
Tính nhanh:
a) $101^2$ ; b) $199^2$ ; c) $47.53.$
Bài giải:
Ta có:
a) $101^2= (100 + 1)^2$
$= 100^2 + 2 . 100 + 1 = 10201$
b) $199^2= (200 – 1)^2$
$= 200^2 – 2 . 200 + 1 = 39601$
c) $47.53 = (50 – 3)(50 + 3)$
$= 50^2 – 3^2 = 2500 – 9 = 2491$.
4. Giải bài bác 23 trang 12 sgk Tân oán 8 tập 1
Chứng minc rằng:
$(a + b)^2 = (a – b)^2 + 4ab;$
$(a – b)^2 = (a + b)^2 – 4ab.$
Áp dụng:
a) Tính $(a – b)^2$, biết $a + b = 7$ cùng $a . b = 12$.
b) Tính $(a + b)^2$, biết $a – b = 20$ với $a . b = 3.$
Bài giải:
– Chứng minh: $(a + b)^2 = (a – b)^2 + 4ab$
+ Biến thay đổi vế trái:
$(a + b)^2 = a^2 +2ab + b^2$
$= a^2 – 2ab + b^2 + 4ab = (a – b)^2 + 4ab$
Vậy $(a + b)^2 = (a – b)^2 + 4ab$ (đpcm)
+ Hoặc cũng rất có thể thay đổi vế phải:
$(a – b)^2 + 4ab= a^2 – 2ab + b^2 + 4ab$
$= a^2 + 2ab + b^2 = (a + b)^2$
Vậy $(a + b)^2 = (a – b)^2 + 4ab$
– Chứng minh: $(a – b)^2 = (a + b)^2 – 4ab$
Biến thay đổi vế phải:
$(a + b)^2 – 4ab = a^2 +2ab + b^2 – 4ab$
$= a^2 – 2ab + b^2= (a – b)^2$
Vậy $(a – b)^2 = (a + b)^2 – 4ab$
Áp dụng:
a) $(a – b)^2 = (a + b)^2 – 4ab$
$= 7^2 – 4 . 12 = 49 – 48 = 1$
b) $(a + b)^2 = (a – b)^2 + 4ab$
$= 20^2 + 4 . 3 = 400 + 12 = 412$
5. Giải bài bác 24 trang 12 sgk Tân oán 8 tập 1
Tính quý hiếm của biểu thức $49x^2 – 70x + 25$ trong những ngôi trường thích hợp sau:
a) $x = 5$; b) $x = frac17$
Bài giải:
Ta có: $49x^2 – 70x + 25$
$= (7x)^2 – 2.7x.5 + 5^2 = (7x – 5)^2$
a) Với $x = 5$ ta có:
$49x^2 – 70x + 25 = (7.5 – 5)^2 = 900$
b) Với $x = frac17$ ta có:
$ 49x^2 – 70x + 25 = ( 7.frac17 – 5)^2 = 16$
6. Giải bài 25 trang 12 sgk Toán thù 8 tập 1
Tính:
a) $(a + b + c)^2$ ;
b) $(a + b – c)^2$;
c) $(a – b – c)^2$
Bài giải:
Ta có:
a) $(a + b + c)^2= <(a + b) + c>^2$
$= (a + b)^2 + 2(a + b)c + c^2$
$= a^2 + 2ab + b^2 + 2ac + 2bc + c^2$
$= a^2 + b^2 + c^2 + 2ab + 2bc + 2ac.$
b) $(a + b – c)^2 = $(a + b) – c>^2$
$= (a + b)^2 – 2(a + b)c + c^2$
$= a^2 + 2ab + b^2 – 2ac – 2bc + c^2$
$= a^2 + b^2 + c^2 + 2ab – 2bc – 2ac.$
c) $(a – b –c)^2= <(a – b) – c>^2$
$= (a – b)^2 – 2(a – b)c + c^2$
$= a^2 – 2ab + b^2 – 2ac + 2bc + c^2$
$= a^2 + b^2 + c^2 – 2ab + 2bc – 2ac.$
Bài trước:
Bài tiếp theo:
Chúc chúng ta có tác dụng bài bác xuất sắc cùng giải bài bác tập sgk toán thù lớp 8 cùng với giải bài xích đôi mươi 21 22 23 24 25 trang 12 sgk toán 8 tập 1!












