Bài tập tự luận về dao động và sóng điện từ có lời giải chi tiết giúp bạn đọc rèn luyện kỹ năng thực hành. và vận đụng tốt kiến thức lý thuyết.Bạn đang xem: Bài tập trường điện từ có lời giải chi tiết
BÀI TẬP DAO ĐỘNG VÀ SÓNG ĐIỆN TỪ CÓ LỜI GIẢI CHI TIẾT
Bài 1: Cho mạch dao động gồm một cuộn dây thuần cảm có độ tự cảm L = 2.10-4H, C = 8pF. Năng lượng của mạch là E = 2,5.10-7J. Viết biểu thức của cường độ dòng điện trong mạch và biểu thức hiệu điện thế giữa 2 bản tụ. Biết O rằng tại thời điểm ban đầu cường độ dòng điện trong mạch có gía trị cực đại.
Lời giải:
Tần số góc \(\omega\) của mạch dao động là: \(\omega =\frac{1}{\sqrt{LC}}=\frac{1}{\sqrt{2.10^{-4}.8.10^{-12}}}=25.10^{6}(rad/s)\)
Biểu thức của điện tích trên tụ điện có dạng: \(q=Q_{0}sin(\omega t+\varphi )=Q_{0}sin(25.10^{6}t+\varphi )\) (1)
\(i=I_{0}cos(25.10^{6}t+\varphi)\)) (2)
Theo đầu bài khi t = 0 ; \(i=I_{0}\rightarrow cos(\varphi )=1\rightarrow \varphi =0\)
Năng lượng của mạch \(E=\frac{L{T_{0}}^{2}}{2}=\frac{{Q_{0}}^{2}}{2C}\) ; \(I_{0}=\sqrt{\frac{2E}{L}}=\sqrt{\frac{2.2,5.10-7}{2.10^{-4}}}=5.10^{-2}(A)\)
\(Q_{0}=\sqrt{2EC}=\sqrt{2.2,5.10^{-7}.8.10^{-12}}=2.10^{-9}C\)
\(\rightarrow i=5.10^{-2}cos(25.10^{6}t)(A)\); \(u=\frac{Q_{0}}{C}sin(25.10^{6}t)=250.sin(25.10^{6}t)(V)\)
Bài 2: Một mạch dao động điện từ lí tưởng đang có dao động điện từ tự do. Tại thời điểm t = 0, tụ điện bắt đầu phóng điện. Sau khoảng thời gian ngắn nhất \(\Delta t\) = 10-6s thì điện tích trên một bản tụ điện bằng một nửa giá trị cực đại. Tính chu kì dao động riêng của mạch.
Lời giải:
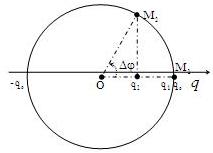
Ở thời điểm đầu (t = 0), điện tích trên một bản tụ là: q1 = qo
Sau khoảng thời gian ngắn nhất ∆t, điện tích trên một bản tụ điện là:
\(q_{2}=\frac{q_{0}}{2}\) ;Ta có: \(\Delta \varphi =\hat{M_{1}OM_{2}}\) Hay: \(\Delta \varphi =\frac{\pi }{3}rad\Rightarrow \Delta t= \frac{\Delta \varphi }{\omega }=\frac{\pi }{3}.\frac{T}{2\pi }=\frac{T}{6}\)
Vậy, chu kì dao động riêng của mạch là: T = 6∆t = 6.10-6s
Bài 3: Một mạch dao động LC lí tưởng đang có dao động điện từ tự do. Điện tích trên một bản tụ điện có biểu thức:
\(q=q_{0}cos(10^{6}\pi t-\frac{\pi }{2})(C)\). Kể từ thời điểm ban đầu( t = 0), sau một khoảng thời gian ngắn nhất là bao lâu thì năng lượng điện trường trên tụ điện bằng ba lần năng lượng từ trường ở cuộn cảm?
Lời giải:

Ở thời điểm ban đầu t = 0, điện tích trên một bản tụ là q1 = 0.
Sau đó một khoảng thời gian ngắn nhất ∆t, thì WL =\(\frac{1}{3}\) WC
\(\Rightarrow W=\frac{1}{3}W_{C}+W_{C}=\frac{4}{3}W_{C}\Leftrightarrow \frac{{q_{0}}^{2}}{2C}=\frac{4}{3}.\frac{{q_{2}}^{2}}{2C}\Rightarrow q_{2}=\frac{\sqrt{3}}{2}q_{0}\) hoặc \(q_{2}=-\frac{\sqrt{3}}{2}q_{0}\)
Ta có:\(\Delta t=\frac{\Delta \varphi }{\omega }\) .với \(\Delta \varphi =\frac{\pi }{2}-\alpha\); mà \(cos\alpha =\frac{q_{2}}{q_{1}}=\frac{\sqrt{3}}{2}\Rightarrow \alpha =\frac{\pi }{6}\Rightarrow \Delta \varphi =\frac{\pi }{3}\).
Vậy: \(\Delta t=\frac{\Delta \varphi }{\omega }=\frac{10^{-6}}{3}(s)\)
Bài 4: Một mạch dao dộng LC lí tưởng có chu kì dao động là T. Tại một thời điểm điện tích trên tụ điện bằng 6.10-7C, sau đó một khoảng thời gian ∆t = \(\frac{3T}{4}\) cường độ dòng điện trong mạch bằng 1,2\(\pi\).10-3A. Tìm chu kì T.
Xem thêm: Vua Hải Tặc Trên Zing Me - Game One Piece Tren Zing Me
Lời giải:
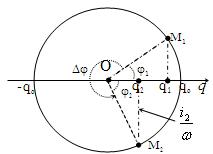
Giả sử ở thời điểm ban đầu t1, điện tích trên tụ điện có giá trị q1. Ở thời điểm t2, sau đó một khoảng thời gian ∆t = \(\frac{3T}{4}\)
ta có \(\Delta \varphi =\omega \Delta t=\frac{2\pi }{T}.\frac{3T}{4}=\frac{3\pi }{2}(rad)\)
Theo giản đồ véc tơ: \(\varphi _{1}+\varphi _{2}=\frac{\pi }{2}\Rightarrow sin(\varphi _{2})=cos(\varphi _{1})=\frac{q_{1}}{q_{0}}\).
Từ công thức: \({q_{0}}^{2}=q^{2}+\frac{i^{2}}{\omega ^{2}}\Rightarrow sin(\varphi _{2})=\frac{i_{2}}{\omega .q_{0}}\)
Do đó \(\frac{i_{2}}{\omega .q_{0}}=\frac{q_{1}}{q_{0}}\Rightarrow \omega =\frac{i_{2}}{q_{1}}=\frac{1,2.\pi .10^{-3}}{6.10^{-7}}2000\pi (rad/s)\) Vậy \(T=10^{-3}(s)\)
Bài 5: Cho mạch dao động điện LC: C = 5\(\mu\)F = 5.10-6F; L = 0,2 H
1) Xác định chu kì dao động của mạch.
2) Tại thời điểm hđt giữa 2 bản tụ u = 2V và dao động chạy qua cuộc cảm i = 0,01 A. Tính I0; U0
3) Nếu tụ C có dạng 1 tụ phẳng, khoảng cách giữa 2 bản tụ d = 1mm, \(\varepsilon\) = 1 thì diện tích đối diện của mỗi bản tụ là?
4) Để mạch dao động thu được dải sóng ngắn từ 10m \(\rightarrow\)50m người ta dùng 1 tụ xoay Cx ghép với tụ C đã có . Hỏi Cx ghép nối tiếp hay song song với C và Cx biến thiên trong khoảng nào?.
Lời giải:
1) Chu kì dao động của mạch: \(T=2\pi \sqrt{LC}=2\pi \sqrt{5.10^{-6}.0,2}=2\pi .10^{-3}(S)\)
2) \(E=E_{đ}+E_{t}=\frac{Cu^{2}}{2}+\frac{U^{2}}{2}=\frac{L{I_{0}}^{2}}{2}=\frac{{U_{0}}^{2}}{2}\)
\(I_{0}=\frac{\sqrt{Cu^{2}+Li^{2}}}{\sqrt{L}}=\frac{\sqrt{5.10^{-6}.4+0,2.(0,01)^{2}}}{\sqrt{0,2}}=0,01\sqrt{2}(A)\)
\(U_{0}=\frac{\sqrt{Cu^{2}+Li^{2}}}{\sqrt{C}}=\frac{\sqrt{4.10^{-5}}}{\sqrt{5.10^{-6}}}=2\sqrt{2}(V)\)
3) Biểu thức tính điện dung C: C = \(C=\frac{\varepsilon .S}{4k\pi d}\) \(\Rightarrow\) Diện tích đối diện của mỗi bản tụ \(S=\frac{C.4k\pi d}{\varepsilon }\)
Thay số \(S=\frac{5.10^{-6}.4.10^{9}.\pi .10^{-3}}{1}=556,2(m^{2})\)
4) Khi chưa ghép Cx: \(\lambda =v.T=3.10^{8}.2.10^{-3}\pi =6\pi .10^{5}(m)\)
Khi ghép Cx: \(\lambda _{X}\) nằm trong khoảng 10m đến 50m nhỏ hơn \(\lambda\)
Lại có \(\lambda _{X}=2\pi v\sqrt{LC_{b}}\Rightarrow C_{b}Vậy Cx nối tiếp với C: \(\frac{\lambda }{\lambda _{X}}=\sqrt{\frac{C}{C_{b}}}=\sqrt{\frac{C.(C_{X}+C)}{C-C_{X}}}=\sqrt{1+\frac{C}{C_{X}}}\)
Bình phương 2 vế: \(\frac{\lambda 2}{{\lambda _{X}}^{2}}=1+\frac{C}{C_{X}}\Rightarrow C_{X}=C.\frac{\lambda 2}{{\lambda _{X}}^{2}}-1\)
+ Khi \(\lambda _{X}=10m\Rightarrow C_{X}=\frac{5.10^{-6}}{\left ( \frac{6\pi .10^{5}}{10} \right )^{2}-1}=1,4.10^{-16}(F)\)
+ Khi \(\lambda _{X}=50m\Rightarrow C_{X}=\frac{5.10^{-6}}{\left ( \frac{6\pi .10^{5}}{50} \right )^{2}-1}=3,5.10^{-15}(F)\)
Kết luận: \(1,4.10^{-16}(F)\leq C\leq 3,5.10^{-15}(F)\)
Bài 6: Mạch chọn sóng của một máy thu vô tuyến điện gồm một cuộc dây có độ tự cảm L và một bộ tụ điện gồm tụ điện chuyển động C0 mắc // với tụ xoay Cx.Tụ xoay có có điện dung biến thiên từ C1= 10pF đến C2= 250pF. khi góc xoay biến thiên từ \(0^{0}\) đến \(120^{0}\). Nhờ vậy, mạch thu được sóng điện từ có bước sóng trong dài từ \(\lambda _{1}\) = 10m đến \(\lambda _{2}\)= 30m. Cho biết điện dung của tụ điện là hàm bậc nhất của góc xoay.
1. Tính L và C0
2. Để mạch thu được sóng có bước sóng \(\lambda _{0}\) = 20m thì góc xoay của bản tụ bằng bao nhiêu?
c = 3.108m/s
Lời giải:
1. Từ Công Thức : \(\lambda =2\pi c\sqrt{LC_{b}}\rightarrow LC_{b}=\frac{\lambda ^{2}}{4\pi ^{2}c^{2}}\)
Khi Cx đạt giá trị C1= 10pF: LC (C1+ C0) = \(\frac{{\lambda _{1}}^{2}}{4\pi ^{2}c^{2}}\)
Khi Cx = C2: L(C2+ C0) = \(\frac{{\lambda _{2}}^{2}}{4\pi ^{2}c^{2}}\)
Thay C1= 10.10-12= 10-11 (pF); C2 = 10-12.250 = 25.10-11 (F) \(\rightarrow\) C0= 2.10-11 (F)
\(L=\frac{{\lambda _{1}}^{2}}{4\pi ^{2}c^{2}(C_{1}+C_{2})}=9,4.10^{-7}(H)\)
\(\lambda _{0}=2\pi c\sqrt{L(C_{0}+C_{3})}\) \(\Rightarrow C_{3}=\frac{{\lambda _{0}}^{2}}{4\pi ^{2}c^{2}L}-C_{0}=10^{-10}(F)=10(pF)\)
2.Kí hiệu \(\varphi\) là góc xoay của bản tụ thì: \(C_{X}=C_{1}+k.\varphi =10+k.\varphi (pF)\)
Khi \(\varphi\) = 0 \(\Rightarrow\) Cx = C1 = 10 (pF)
Khi \(\varphi\) = 1200 \(\Rightarrow\) Cx = 10 + k.120 = 250 (pF) \(\Rightarrow\) k = 2.
Như vậy Cx = 10 + 2\(\varphi\)
Khi \(\lambda =\lambda _{0}\) thì Cx = C3= 100 (pF) \(\Rightarrow \varphi =45^{0}\)
Tụ điện ghép:
Bài 7: Khung dao động gồm cuộn L và tụ C thực hiện dao động điện từ tự do, điện tích cực đại trên 1 bản tụ là
Q0 = 10-6C và chuyển động dao động cực đại trong khung là I0 = 10A.
a. Tính bước sóng của dao động tự do trong khung
b. Nếu thay tụ điện C bằng tụ C" thì bước sóng của khung tăng 2 lần. Hỏi bước sóng của khung là bao nhiêu nếu mắc C" và C song song, nối tiếp?
Lời giải
a. Tính bước sóng
Năng lượng điện từ trong khung dao động
\(E=E_{đ}+E_{t}=\frac{q^{2}}{2C}+\frac{1}{2}.Li^{2}\) \(E=E_{đmax}=E_{tmax}\rightarrow \frac{{Q_{0}}^{2}}{2C}=\frac{L.{I_{0}}^{2}}{2}\)
Do đó \(LC=\frac{{Q_{0}}^{2}}{{I_{0}}^{2}}\Rightarrow \sqrt{LC}=\frac{Q_{0}}{I_{0}}\)
Bước sóng : \(\lambda =2\pi \sqrt{LC}=2\pi .3.10^{8}.\frac{10^{-6}}{10}\approx 188,4(m)\)
b. Bước sóng của khung
+ Khi có tụ C: \(\lambda =2\pi c\sqrt{LC}\)
+ Khi có tụ C" : \(\lambda =2\pi c\sqrt{LC"}\)
\(\frac{\lambda }{\lambda ^{"}}=\sqrt{\frac{C}{C"}}=\frac{1}{2}\Rightarrow \frac{C}{C"}=\frac{1}{4}\Rightarrow C"=4C\)
+ Khi C nt C": \(C_{b1}=\frac{C.C"}{C+C"}=\frac{4C^{2}}{5C}=\frac{4}{5}C\)
Bước sóng \(\lambda _{1}=2\pi \sqrt{L.\frac{4}{5}.C}=\frac{1}{\sqrt{5}}\pi c\sqrt{LC}=\frac{2}{\sqrt{5}}\lambda \Rightarrow \lambda _{1}=168,5(m)\)
+ Khi C // C": Cb2= C + C" = 5C
Bước sóng \({\lambda _2} = 2\pi \sqrt {5LC} = \sqrt 5 {\lambda _1} = 421,3(m)\)
Tải về
Luyện Bài tập trắc nghiệm môn Vật lý lớp 12 - Xem ngay












